Articles → Torispherical Head Volume and Weight

Torispherical Head Volume and Weight

We've unlocked the Shell & Head Design module for testing. Give it a try!

As there's no step-by-step calculation or a single equation to calculate the volume and weight of a torispherical head in the ASME BPVC code, we had to find how to do it ourselves. Luckily we found an article in the Wolfram MathWorld [ 1 ] that helped us a lot. Below we'll explain how we used it to find out the inside volume and weight of the torispherical head used in the Shell & Head Design module.

The reason we don't put the equation in the Results page is because, as you'll see, it gets a little complicated and such calculation isn't required by ASME (to be honest, it's so easy to get the volume and weight using any CAD software that we believe many Users will just ignore the calculated value)

1. What's a Torispherical Head?

According to Wolfram MathWorld:

A torispherical dome is the surface obtained from the intersection of a spherical cap with a tangent torus, as illustrated above. The radius of the sphere R is called the crown radius, and the radius a of the torus called the knuckle radius. torispherical domes are used to construct pressure vessels.

2. Torispherical Head Inside Volume

Fig. 2.1 - Torispherical Head Dimensions

Again, according to Wolfram MathWorld, the equation to find the volume (V_head or V2 in the Fig. 3.1.) of a torispherical head is:

$$\begin{align}V_{head} = {{\pi \over 3}\Big[2hR^2-(2a^2+c^2+2aR)(R-h)+3a^2csin^{-1}{(R-h)\over(R-a)}\Big]}\tag{1}\end{align}$$

To find the head height (h):

$$\begin{align}h = {{R - \sqrt{(a + c - R)(a - c - R)}}}\tag{2}\end{align}$$

Where:

R crown radius (it's the L variable in the ASME BPVC Section VIII Division 1)
h head height (calculated);
a knuckle radius (it's the r variable in the ASME BPVC Section VIII Division 1)
c distance from the center of the head to the center of knuckle radius (D / 2 - r, where D is the head inside diameter and r is the knuckle inside radius as stated above)

The Equation (1) don't take in account the straight flange of the head (V3 in Fig. 1.2):

$$\begin{align}V_{flange} = {{\pi \cdot D^2 \over 4} \cdot b}\tag{3}\end{align}$$

Where:

D inside diameter
b straight flange height

Now we can calculate the total inside volume of the head:

$$\begin{align}V_{total-inside} = {V_{head} + V_{flange}}\tag{4}\end{align}$$

3. Torispherical Head Weight

To calculate the torispherical head weight we must also calculate the total outside volume. To do that we'll use the equations (1) to (4) changing inside dimensions to outside (we used the subscription o to specify outside) by adding the head thickness. V_head-outside is the same as V1 in the Fig. 3.1. and V_{flange-outside} is the same as V4.

Fig. 3.1 - Torispherical Head Volumes

$$\begin{align}V_{head-outside} = {{\pi \over 3}\Big[2h_{o}R_{o}^2-(2a_{o}^2+c_{o}^2+2a_{o}R_{o})(R_{o}-h_{o})+3a_{o}^2c_{o}sin^{-1}{(R_{o}-h_{o})\over(R_{o}-a_{o})}\Big]}\tag{5}\end{align}$$ $$\begin{align}h_{o} = {{R_{o} - \sqrt{(a_{o} + c_{o} - R_{o})(a_{o} - c_{o} - R_{o})}}}\tag{6}\end{align}$$ $$\begin{align}V_{flange-outside} = {{\pi \cdot D_{o}^2 \over 4} \cdot b}\tag{7}\end{align}$$ $$\begin{align}V_{total-outside} = {V_{head-outside} + V_{flange-outside}}\tag{8}\end{align}$$

To find the actual total volume (V5 + V6 from Fig. 3.1.) we must subtract V_total-inside from V_{total-outside}, after that the weight can easily be found by multiplying the result by the material density as shown in equation (9).

$$\begin{align}Wg = {{(V_{outer} - V_{inner}) * density}}\tag{9}\end{align}$$

If you are designing the head according to ASME BPVC, the material density can be found in ASME BPVC Section II[ 2 ] tables. We also have a ASME Material Database module that can help you with that.

4. Calculation Checking

To check if our equations are correct, we'll compare it with a CAD (Computer Aid Design) software, in this case, AutoCAD 2016[ 3 ].

Consider the following:

R (inside crown radius) = 1000 mm
a (inside knuckle radius) = 150 mm
c (distance from the center of the head to the center of knuckle radius) = 350 mm
t (plate thickness) = 40 mm
b (straight flange height) = 60 mm
density = 8000 kg/m^3

If c = 350 and a = 150, then D (inside diameter) = 1000 mm.

Results using equations (1) to (9):

V_total-inside = 168354363.656 mm^3
V_{total-outside} = 223187593.836 mm^3
Wg = 438.67 kg

As you can se in Fig. 4.1 and 4.2, we got exactly the same result as CAD.

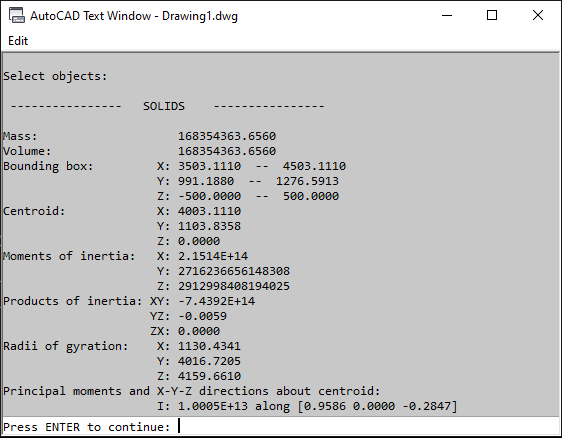Fig. 4.1 - AutoCAD 2016 Output for Inner Volume

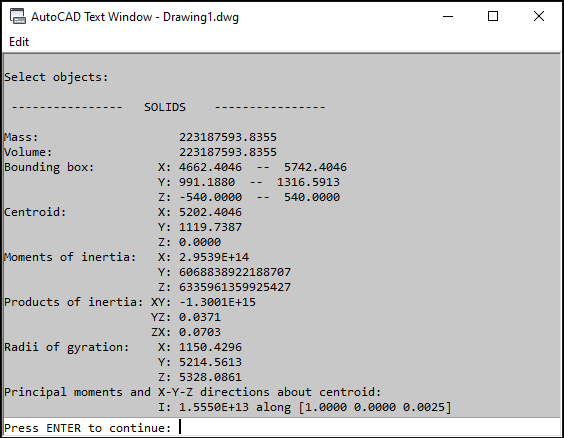Fig. 4.2 - AutoCAD 2016 Output for Outer Volume

5. Shell & Head Design Module

If you are using the Shell & Head Design module, you'll see the torispherical head weight in the Summary (see Fig. 5.1) and in the equations part (see Fig. 5.2). As the calculation have many steps and it isn't required by the ASME BPVC Section VIII Division 1, we decided to not show it in the results page. Instead, the User will see a link to this article (in case someone want to make sure that the result is correct).

Fig. 5.1 - SHD Module, Summary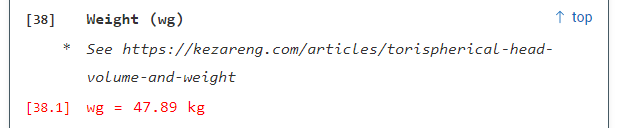

Fig. 5.2 - SHD Module, Results Page

Oh, in case you really need to show the calculation steps in the results page, send us a message through Contact page and we'll see what we can do. Maybe, if we get enough requests, we'll add it in the next update.

Changelog

To see the changelog entries just click in the arrow next to Changelog title.

If you want to receive an e-mail notification every time an article or documentation is updated, just sign up and click in the Notify Me button at the bottom of the page (only visible for logged Users).